Profundicemos un poco en la historia del poker. El entrenador de Red Chip Poker, Adam w34z3l, recordó los teoremas que fueron inventados por nuestros antepasados en la década de 2000. Según él, en aquellos tiempos maravillosos, estos teoremas eran conocidos por todos los que se consideraban profesionales. Bueno, o viceversa, los que conocían estos teoremas se consideraban profesionales.
Adam comprobó si estos antiguos conocimientos secretos han pasado la prueba del tiempo y si se puede adaptar a las realidades modernas. En el lado positivo, son mucho más fáciles de recordar que la frecuencia correcta de la apuesta de continuación en un bote de 3-bet, pero en el lado negativo, no todos funcionan a la perfección. Sin embargo, lo mismo sucede con todos estos solvers..
Teorema de Baluga
Este teorema no se trata de los peces grandes de la familia del esturión, sino de subidas en el turn. Fue formulado por Andrew BalugaWhale en 2006 en 2+2. Suena así:
La fuerza de un par debe reevaluarse significativamente después de una subida en el turn
Ejemplo original de 2006:
Estamos UTG con AKo, subiendo a 4bb (puedes sentir la vibra de la vieja escuela de inmediato). BTN iguala, el flop viene A93o. Hacemos una apuesta del tamaño del bote (ahora el solver aconseja apostar mucho menos), el oponente paga. El turn es un 7 para un proyecto de color. Apostamos el bote de nuevo y nos suben.
El teorema de Baluga es que después de estas subidas, nuestro top pair con top kicker no se ve muy bien. El teorema no dice que debes retirarte, solo que debes ser muy crítico con la fuerza de tu mano. Bueno, y a veces también decir “paso”, ya que a menudo resultará ser la decisión correcta.
Si analizamos esta situación en el solver, casi siempre aconseja igualar tanto una subida en el turn como una apuesta en el river. Sin embargo, debe entenderse que después de apostar en el river, nuestro TPTK es solo un bluff catcher. El EV de igualar en el turn no es muy alto, técnicamente es un call que jugamos para proteger nuestro rango, de lo contrario terminamos foldeando demasiado en el turn. Si en esta situación nuestra mano es más débil que TPTK, entonces el solver tenderá a retirarse.
En general, este teorema está bastante alejado de GTO y está más orientado a un exploit. Su idea es que el oponente promedio no suele farolear con una subida en el turn. Si miras Range Research para ver con qué se está raiseando el turn en NL200 de PokerStars en estos días, se ve así:
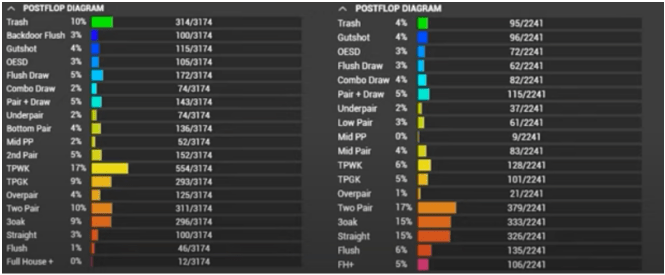
El 58% de las veces, el oponente promedio tendrá dos pares o más después de un check-raise, y el 70% de las veces tendrá un par máximo o más. Si el oponente está en posición, entonces el valor de sus manos será casi la mitad: 25% de dos pares y más, y 30% pares superiores o más.
En general, podemos decir que el teorema de Baluga todavía funciona. Sin embargo, debes tener en cuenta que es mucho más rentable usarlo contra los check-raises, ya que los jugadores en posición a menudo aumentan con bluffs y semi-bluffs.
Teorema de Clarkmeister
Este teorema también nació en 2+2. Suena así:
Si una cuarta carta del mismo palo aparece en el river heads-up y tenemos la primera palabra, debemos apostar
Suena bastante lógico. Es cierto que es bastante difícil probar el beneficio o el daño de este teorema, ya que aquí todo depende de la situación específica.
Por ejemplo, estamos fuera de posición, nuestro oponente hace una apuesta de continuación en el flop y en el turn, y la cuarta carta de color llega en el river. En esta situación, nuestro bluff donk en el river genera un 57% de fold equity, y aplicar el teorema de Clarkmeister será muy rentable: si apostamos el 75% del bote, entonces necesitamos obtener solo el 40% de fold para convertir esta acción en lucrativa.
Otro escenario adecuado para el teorema es cuando estamos haciendo probe. Este es el nombre de una apuesta que realizamos contra un oponente que no realizó una apuesta de continuación en una o más de las calles anteriores. Aquí nuestra apuesta en el river ya dará un 62% de equity. Sin embargo, esta situación es mucho menos reveladora, ya que casi siempre tenemos mucho fold equity aquí, independientemente de la carta que haya salido en el river. Pero en el primer caso, la cuarta carta del color es importante, ya que en otra situación el donk no será tan rentable.
Esto no significa, por supuesto, que el teorema funcione perfectamente. Si apostamos tres veces fuera de posición, haciendo c-bet en el flop, el turn y el river, en la mayoría de los casos nuestro fold equity en el river caerá al 40%. Además, la opción en la que la cuarta carta del color sale en el river, es incluso peor que las otras; en otros casos, nuestro fold equity es del 45-50%.
Conclusión: se puede considerar que el teorema de Clarkmeister funciona, pero no en todas las situaciones. GTO no es tan optimista sobre este teorema y rara vez aconseja apostar en la cuarta carta de color.
Teorema de Yeti
Este teorema también surgió sobre 2+2 y recibió el nombre en honor al autor.
Un 3-bet en un flop seco, especialmente en un flop emparejado, es casi seguro un farol
Digamos que encontramos el flop A72o o KK2o. Nuestro oponente hace una apuesta de continuación, nosotros subimos. Si hace otra subida, será difícil creer en la fuerza de su mano. En la mayoría de los casos, con tríos de reyes o un trío de sietes, al ver una subida, casi todos los oponentes jugarán lento. Pero si todas las manos fuertes en las mesas secas se vuelven lentas, ¿cómo estaría compuesto un rango de 3-bet? ¿Es todo de bluff? Esto parece un gran problema en estos días. Y si observas el software, resulta que en estos días este teorema simplemente no es cierto.
Ahora, el rango de 3-bet bluff en el flop del jugador promedio es casi inexistente, y sólo jugará de esta manera con las nueces de hierro, independientemente de la textura. En una muestra con NL200 en una mesa seca o emparejada, el porcentaje de bluff, 3-bet y fusiones es extremadamente bajo.
Conclusión: El Teorema de Yeti no ha pasado la prueba del tiempo. Existe la sospecha de que incluso en 2005 no estaba imprimiendo dinero precisamente...
Teorema de Zeebo
Ningún jugador es capaz de foldear un full house, sin importar la calle o el tamaño de la apuesta
Aquí, incluso sin análisis, podemos decir que estos son cuentos de hadas. En la situación correcta, deshacerse de un full no es tan difícil, hay jugadores así y hay muchos de ellos. Especialmente cuando hay dos parejas en la mesa y tenemos un full bajo.
Por ejemplo, tomemos el board 8877x. Si tenemos 7x y el villano está apostando mucho, se puede considerar retirarse en esta situación. Sin embargo, esto no hace que el teorema sea inútil. Parafraseándolo un poco, puede servir bien ahora:
No intentes sacar a los jugadores del bote si sospechas que tienen una mano fuerte
Si asume que su oponente tiene un full house, entonces no debe farolear. Esto se aplica tanto a las escaleras como a los colores, a menos que haya una historia de fondo que te permita creer que tu oponente es capaz de realizar un fold difícil. Esta definitivamente no es una situación en la que puedas ganar dinero.
Otra lección relevante que podemos aprender de este teorema es que es más probable que un jugador desconocido sobreestime la fuerza de su mano. Alguien mirará sus cartas y pensará: "¡Guau, tengo un full house!" Incluso si este full está dominado por todos lados, confiarán en la fuerza absoluta de su mano, sin prestar atención a todo lo demás. Incluso hoy en día, hay muchos jugadores de este tipo en las mesas, especialmente en los niveles micro.
Teorema de AEJones
Fue publicado por el high roller aejones en el foro 2+2 en 2007.
Nadie nunca tiene nada
Por supuesto, esta sabiduría de siglos pasados no debe tomarse literalmente, por supuesto, pero este teorema se puede reformular de la siguiente manera:
Los jugadores no siempre tendrán una mano tan fuerte como crees
Este problema se puede llamar el síndrome del "monstruo debajo de la cama". Por lo general, aumenta durante las malas rachas, cuando constantemente ves las nueces en tus oponentes. "¡Por supuesto que hiteamos un set bajo, pero el enemigo debe tener un set superior!" No es difícil creer en esto, especialmente si estas situaciones te han sucedido con bastante frecuencia en las últimas decenas de miles de manos.
Si tratamos de ignorar el efecto de las rachas y miramos el panorama general, resulta que la mano del oponente es a menudo más débil de lo que pensábamos. No es fácil hacer una mano fuerte en Hold'em, y si nosotros no siempre lo hacemos bien, nuestros oponentes deben tener el mismo problema. Es útil recordar esto, especialmente durante una mala racha.
De esta afirmación se puede deducir una más, que no pierde su relevancia a través de los tiempos:
El juego agresivo es mucho más rentable que el juego pasivo
No te preocupes demasiado por el hecho de que tu oponente tenga una mano fuerte en algún caso particular, porque esto puede evitar que te decidas por un farol rentable en la próxima mesa. Y a veces incluso te sorprenderá la facilidad con la que los oponentes están dispuestos a deshacerse de sus cartas.
Eso es todo acerca de los antiguos teoremas. Espero que hayas disfrutado nuestro viaje por el camino de la memoria, y qué diablos, tal vez incluso hayas aprendido algo al hablar sobre los principios que se consideraban inquebrantables en la era antigua del poker en línea.












