Hago muchos vídeos de poker y puedo decir con autoridad que de todos los términos de la teoría del poker, el que la gente menos entiende es la frecuencia mínima de defensa: MDF. Parece bastante simple: MDF te dice qué tan ampliamente debes defenderte para que tu oponente no pueda bluffear de manera rentable con cualquier mano. Sin embargo, existen muchos mitos en torno a este sencillo concepto que dificultan su uso correcto. Hoy intentaremos corregir la situación.
Empecemos por los casos más sencillos.
– Los principiantes suelen confundir MDF con pot odds. Ambos describen riesgo y recompensa, pero el primero es sobre bluffear y el segundo es sobre dar call.
– Se producen errores al calcular el MDF cuando recibimos una subida: la gente sustituye valores en la fórmula incorrecta. Sin embargo, ya grabé un vídeo sobre esto y no quiero repetirlo hoy.
Mi tema de hoy son los mitos y los errores conceptuales.

He visto cálculos de MDF que no tienen en cuenta que los bluffs tienen equit. Esto a menudo se debe al cálculo de las tendencias del field. Los autores analizan los datos y dicen: ¡mira, el field foldea con más frecuencia que el MDF! ¡Esto significa que podemos bluffear con dos cartas cualesquiera! Desgraciadamente, se equivocan o utilizan la fórmula equivocada. Cuando los bluffs tienen equity, el MDF se calcula de manera diferente.
Los jugadores de poker más experimentados te dirán que un solver que juega GTO siempre defiende menos que MDF. Entiendo por qué la gente piensa así, pero tampoco es cierto. Y hoy lo veremos.
Por último, se suele decir que el MDF no importa hasta el river. Parece que se trata de una métrica primitiva, inventada para juegos con reglas reducidas en los que los bluffs no tienen equity, es decir, no se puede utilizar en ninguna calle excepto en la última. Si usted también cree esto, quizás el problema sea que esté utilizando una definición demasiado simplificada de MDF.
Hablemos de las complejidades del análisis de grandes bases de datos. Si han estado jugando durante mucho tiempo, almacenando todas sus manos e intentando determinar las tendencias del field a partir de esta base de datos, comparando las acciones de los jugadores con MDF, probablemente notará que
1) el field overfoldea a las apuestas de continuación del flop;
2) el field defiende demasiado amplio contra una subida en el flop.
Esto nos lleva a una estrategia explotativa de apuestas de continuación con dos cartas cualesquiera... pero no, no es una idea muy viable. ¿Por qué? Sí, porque ese juego del field es absolutamente correcto y, además, corresponde a GTO. Ahora veremos esto.
Digamos que hijack subió y la ciega grande pagó. Los stacks son de 100 bb. El flop... no importa cuál sea el flop, porque estoy usando las estadísticas agregadas de todos los flops. El hijack hace una c-bet del 33% del bote.
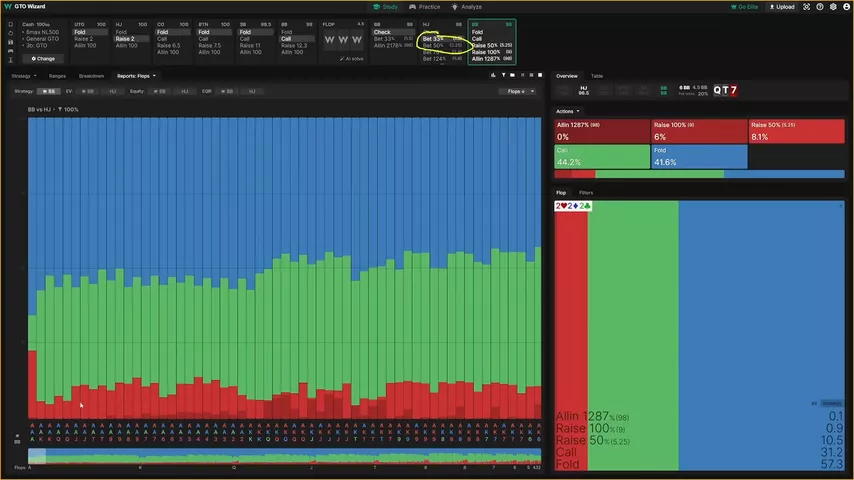
Y la ciega grande se retira el 41.6% de las veces. Atención, pregunta: ¿cuál es la frecuencia mínima de defensa para un jugador en la BB frente a una apuesta de 1.5 BB en un bote de 4.5 BB?
Alfa = 1.5 / (1.5 + 4.5) = 25% (fold)
MDF = 1 – alfa = 75 % (defensa)
Si hicimos los cálculos correctamente, deberíamos tener un MDF "ingenuo" para la ciega grande del 75%. ¡Pero el solver foldea mucho más!
¿Que está sucediendo? ¿Es el solver un nit espeluznante?
Busquemos el flop donde la BB defiende más. Este será el flop . Sin embargo, incluso en este caso, la BB foldea en el 27.8% de las manos.
La razón es realmente muy lógica. Tomemos un flop, digamos , y observemos el valor de la mano más débil en el rango de hijack versus el rango de la BB. : bueno, sí, no se ve muy bien en tal flop. Sin embargo, su equity es del 21.8%. Esto significa que, incluso con , quien subió antes del flop puede dar check por detrás y obtener parte de esa equity. Resulta que no tiene ningún bluff puro en el flop.
Como recordarán, el MDF está diseñado para hacer que su oponente sea indiferente a la hora de elegir entre un bluff y un check. Pero incluso con la mano más débil en el rango de hijack, el EV del check es bastante alto: 1.66bb. Si empezamos a defender desesperadamente, el EV de un bluff con se vuelve igual a cero, nuestro oponente simplemente dejará de bluffear con esa mano y realizará tranquilamente parte de la equity a través de un check, mientras al mismo tiempo te destruye con apuestas adicionales con otras manos.
Entonces, cuando el field overfoldea frente a una c-bet en comparación con MDF, está haciendo lo correcto.
Pasemos ahora al segundo punto. Veamos las estadísticas resumidas de todos los flops para el caso en el que el highjack hizo una c-bet de 1.5 BB y recibió una subida de 9 BB. Primero, calculemos el MDF: ¿con qué amplitud se debe defender en jugador en hijack?
Alfa = 9 / (9 + 6) = 60% (fold)
MDF = 1 – alfa = 40% (defensa)
Si las matemáticas están bien, tomamos la cantidad de fichas que arriesga la BB y la dividimos entre riesgo + recompensa. Resulta que la ciega grande necesita que el highjack se retire el 60% de las veces. El 40% queda para la defensa.
En la práctica, nada de esto sucede.
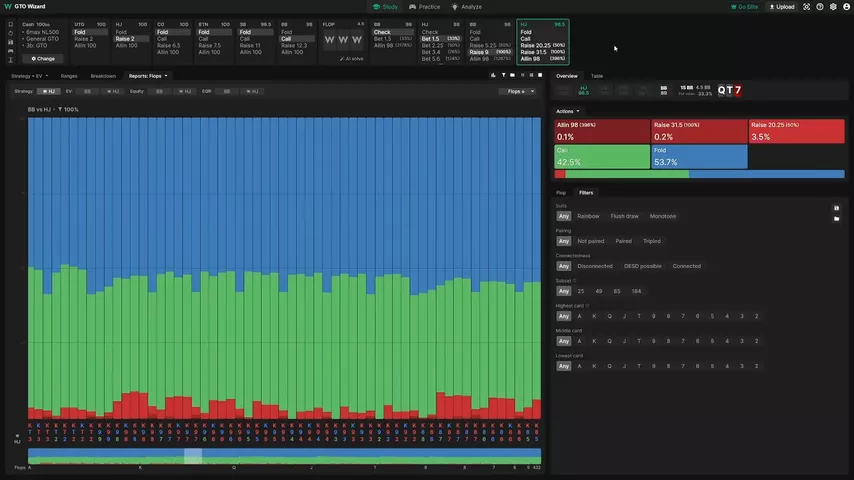
Hijack foldea notablemente menos que el 60% e iguala más del 40%. Si la gente de su base se defiende contra subidas de manera amplia que lo que dicta el MDF, tienen razón.
Para ilustrar, tomé el flop .
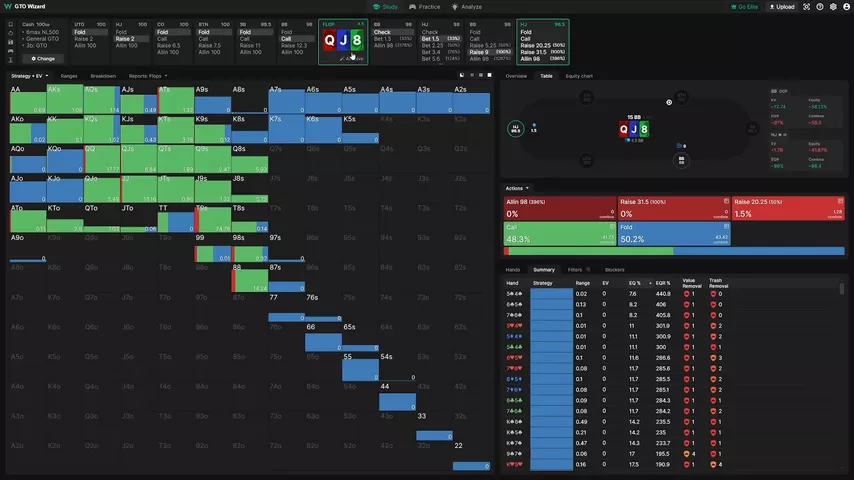
Hijack iguala una subida notablemente más amplio que el 40%. Y la razón es que los bluffs tienen equity.
Ordenemos el rango la BB y encontremos la mano con el valor más bajo. Esta mano será – ¡Pero incluso esa mano tiene un 8.4% de equity! No muy a menudo, pero también puede ganar el bote en el showdown.
Si el hijack comienza a foldear en MDF, el jugador en la BB, quien ahora siempre está foldeando ¡Podrá hacer check-raise con esa mano! Después de todo, nuestro oponente se retira con suficiente frecuencia como para que el EV del bluff sea cero, y luego obtenemos un freeroll con un 8.4% adicional de equity a partir del turn. Y lo mismo ocurre con todas las manos en las que la BB se retira ante una c-bet. Ahora foldea todas las combinaciones de A4s, y esas combinaciones tienen un equity enorme del 25%. ¿Por qué no subir con ellas como un bluff?
Toda esta historia de bluffs que tienen equity sucederá en todas las calles hasta el river. La frecuencia de la defensa del GTO contra una subida siempre será mayor que la del MDF porque no debemos darle un freeroll a los bluffs por el monto de su equity.
Ahora utilizaré un informe completo que muestra la reacción al conjunto de tamaños más amplio posible y que es perfecto para mi tarea. Se debe activar en las opciones de GTO Wizard (icono en la esquina superior derecha).
Una vez que tengo los datos que necesito, creo un gráfico que compara el porcentaje de folds de GTO con el porcentaje de folds de MDF dependiendo del tamaño de la c-bet.
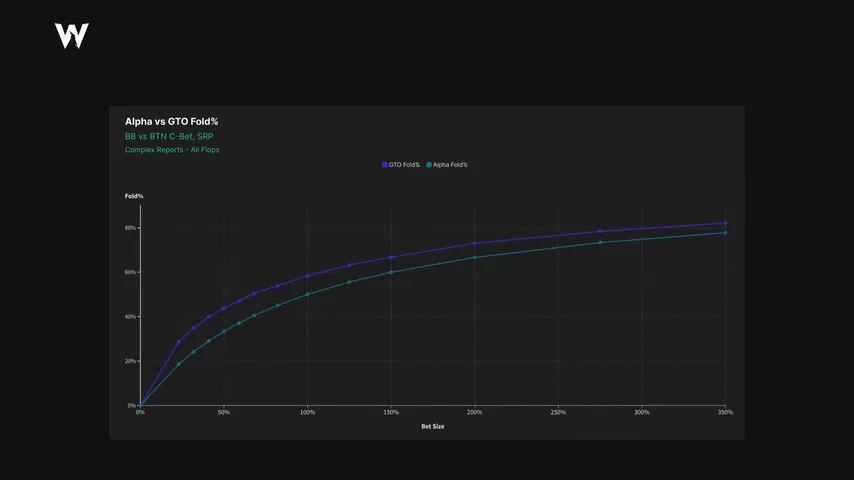
Como era de esperar, la ciega grande siempre foldea más que MDF (línea azul vs. línea azul claro), independientemente del tamaño.
¿Está resuelto el problema?
Cambiemos de posición y veamos cómo reacciona la ciega grande a las c-bets de la ciega pequeña.
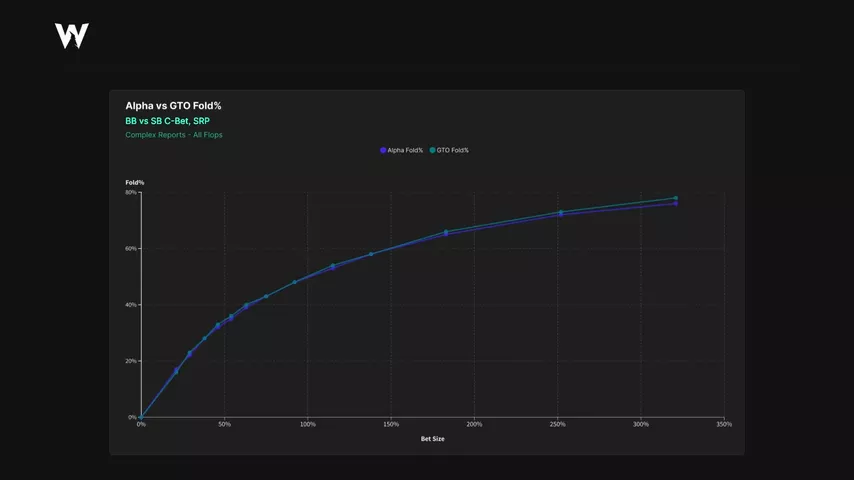
¿Entiendes cuál es la diferencia? En este ejemplo, la ciega grande está en posición. Y la posición da una ventaja. Mientras está en posición, la BB defiende casi estrictamente según MDF.
Entonces, si su objetivo es jugar GTO, deben overfoldear fuera de posición y jugar cerca de MDF mientras estén en posición.
Las matemáticas del verdadero MDF

Calcular el EV de un bluff puro (un bluff con cero equity) es bastante sencillo:
EV = (frecuencia de fold * tamaño del bote) – (frecuencia de call * tamaño de nuestro bluff)
Cuando apostamos dos botes en el river, obligamos a nuestro oponente a defender el 34% de sus manos. Tan pronto como comienza a foldear de más, nuestro bluff imprime dinero. Si defiende más ampliamente, el bluff pierde dinero.
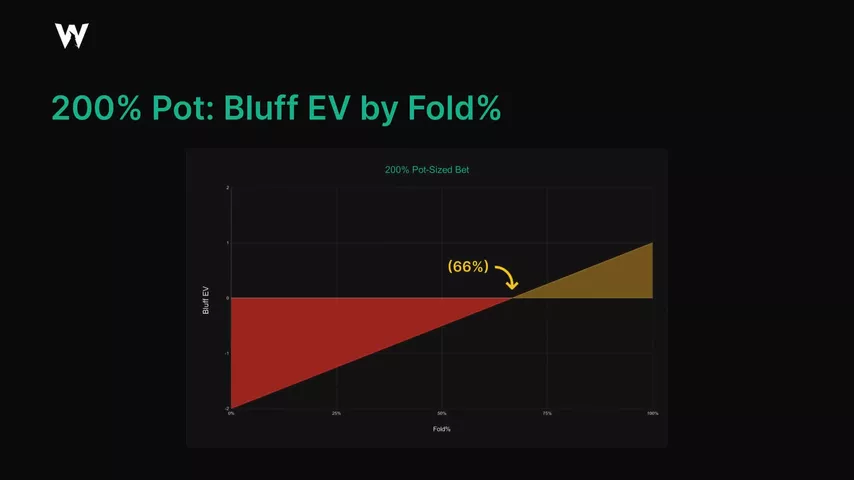
Cuando apostamos 2/3 del bote, el oponente debe defender un poco más: no el 34%, sino el 60%. La fórmula es elemental.
Sin embargo, todo cambia cuando aceptamos que los bluffs tienen equity.
Comparemos el MDF ingenuo y el MDF verdadero:

Los bluffs a los que les pagan siempre pierden.
El check siempre pierde.
La única forma de ganar es obligar a su oponente a retirarse.
EV de un bluff = 0
– Los faroles que reciben un call retienen algo de equity
– El EV de un check es superior a cero
– Los bluffs se pueden retrasar hasta la siguiente calle
– EV de un farol = EV de un check
Digamos que nos encontramos en el river con una mano que a veces ganará en el showdown. Por ejemplo, con un par en mano débil que vence a algunas de las manos del oponente. Nos preguntamos si convertirlo en un bluff apostando la mitad del bote.
Digamos que nuestra mano ganará en el showdown el 25% de las veces. ¿Con qué frecuencia nuestro oponente tiene que retirarse para que el bluff sea más rentable que un check?
EV del bluff = EV del check = 25%
25% = frecuencia de fold * bote – frecuencia de call * tamaño de la apuesta
25% = (1 – x) (1) – 0.5x
La frecuencia de call deseada es del 50%.
El MDF ingenuo considera que la expectativa de un check es cero, en cuyo caso el oponente sólo necesita retirarse el 33.3% de las veces. Sin embargo, cuando nuestro bluff tiene algún valor, necesitamos mucha más fold equity para hacerlo de forma rentable.
De hecho, debemos tener en cuenta no sólo la probabilidad de un fold y de un call, sino también de una subida: también tenemos EV contra una subida. Pero en aras de la simplicidad, supongamos que esto no sucede.
MDF ingenuo: EV de un check = 0:
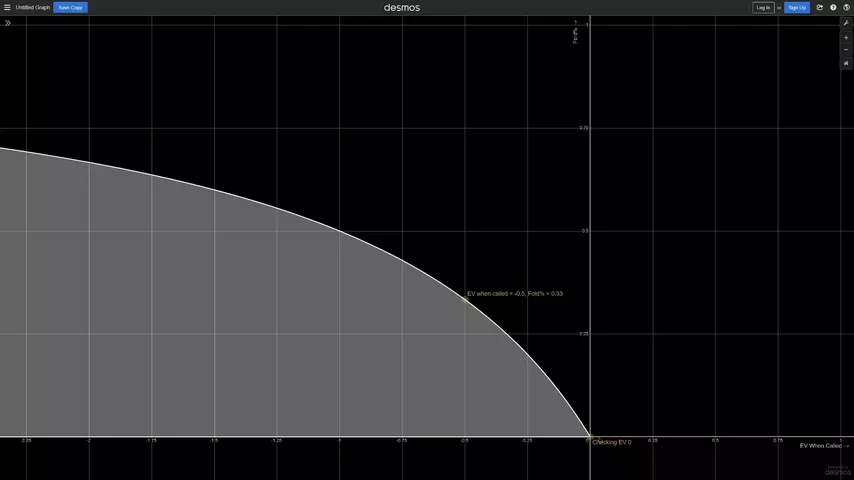
Ahora elevemos el EV del check (eje Y):
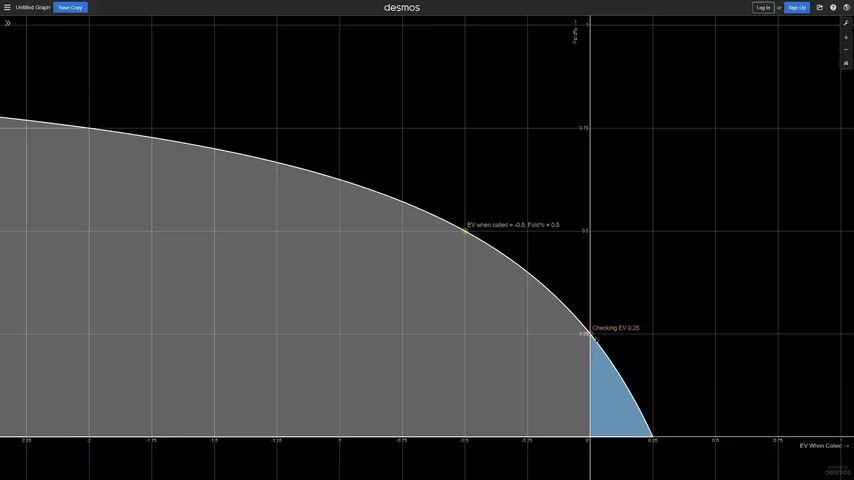
Es lógico: cuanto mayor sea el EV del check, más equity necesitamos para un bluff rentable.
Presten atención a la zona azul a la derecha del eje Y: son manos en las que se trata de apuestas por valor, es decir, tienen una expectativa positiva, pero pasar con ellas es más rentable. No todas las acciones +EV son óptimas.
Proporción áurea?!?!
Finalmente, una pequeña ventaja.
La frecuencia de defensa del solver contra una subida en el flop, por extraño que parezca, se puede encontrar utilizando una fórmula bastante simple, en una sola acción:
Porcentaje de fold de GTO vs. una subida aproximadamente igual a las probabilidades del bote * proporción áurea : 1.618
No puedo imaginar de dónde viene esta dependencia, pero funciona: la diferencia con el valor real es sólo del 2-3%.
Digamos que apostamos un tercio del bote y obtenemos una subida de la mitad del bote. Las pot odds son del 25%. Frecuencia de fold aproximada = 0.25*1.618 = 0.4045 o 40.6%. Frecuencia de fold real según GTO = 38.3%.
Hagamos una subida del tamaño del bote. Las pot odds son del 33%. Frecuencia estimada = 0.33*1.618 = 0.538794 o 53.9%. Frecuencia verdadera = 54.3%.
¡Milagros!
- Mayor rakeback y bonos personales
- Ayuda con depósitos y retiros
- Acceso a aplicaciones móviles
- Resolvemos problemas con cuentas
- Soporte técnico
- Preguntas acerca del sitio y el foro





















