El bluff es una habilidad fundamental en el poker que combina el engaño y el cálculo estratégico para cambiar el rumbo de una mano. Las matemáticas básicas que forman la base de los bluffs se tratan en muchos artículos y libros. Los bluffs largos de tres barriles no tienen tanta suerte.
En este artículo veremos las matemáticas de los bluffs largos, es decir, el método para calcular la expectativa (EV) de un bluff de varias calles.
Conceptos básicos: Bluff de una calle
El cálculo es muy sencillo. Encontramos la frecuencia mínima de defensa (MDF). Si tu oponente se retira con más frecuencia que 1 – MDF, el bluff será rentable. La expectativa de un bluff puro (es decir, sin outs para mejorar) se calcula de la siguiente manera:
EV (bluff) = %fold*(tamaño del bote) – %call*(tamaño de la apuesta)
Si el EV está por encima de cero, incluso un bluff puro genera dinero.
¡Es sencillo! Pero hay un matiz. Si nuestro oponente iguala pero las calles de apuestas aún no han terminado, no estamos obligados a rendirnos y podemos seguir bluffeando en las calles siguientes.
¿Esto qué cambia?
Tarea
Comprobemos su comprensión intuitiva con un ejemplo simplificado:
Tiene un bluff puro en el flop y está pensando en hacer tres barriles en esta mano (el tamaño de la apuesta en cada calle es de un bote completo). Su oponente siempre igualará en el flop y el turn. ¿Con qué frecuencia tiene que foldear en el river para que nuestro bluff alcance el punto de equilibrio?
A) 50%
B) 61%
C) 72%
D) 83%
Respuesta correcta:
c) 72%
He visto a jugadores responder (a) porque eso es lo que sucede cuando se calcula el MDF en el river. Sin embargo, se olvidan de contar el dinero que invirtieron en bluffear en el flop y en el turn. Para que los tres barriles sean rentables, nuestro bluff en el river no debería ser cercano a cero, sino tan positivo como para compensar todas nuestras pérdidas anteriores.
Entonces, para apostar tres barriles de manera rentable, necesitamos mucho fold equity en el river. Calculemos exactamente cómo se obtiene este número.
El tamaño del bote inicial es 1. Apostamos 1 en el flop, 3 en el turn y 9 en el river. Si el oponente llega al showdown, perdemos 13 botes iniciales. Si la mano se termina en el river, ganamos 5 botes (1+1+3). 13 / (13 + 5) = 72.2%.
Como puede ver, la relación riesgo/recompensa de los bluffs largos es peor que la de los bluffs cortos porque estamos poniendo más fichas que las que esperamos recuperar.
Está claro que éste no es un ejemplo del todo justo. Nadie iguala con todo su rango en el flop y turn solo para retirarse con el 3/4 de sus manos en el river. Nuestro próximo ejemplo será más realista, pero también más complejo.
Déjeme decirle de inmediato: no debe hacer estos cálculos durante el juego. Practíquelos en casa durante la preparación y utilice una calculadora online para calcular los límites de fold.
Tres asunciones que tendremos en cuenta a la hora de calcular:
1. Cuando pasa, siempre pierde
2. Cuando su oponente llega al showdown, siempre pierde
3. Su oponente nunca sube, sólo iguala o foldea
Veamos cuatro estrategias:
1. Check y darse por vencido, minimizando pérdidas
2. Bet, check: hacer una apuesta y darse por vencido si le pagan
3. Bet, bet, check: apostar dos barriles como bluff, pero no seguir adelante con el bluff
4. Tres barriles: ¡sin dar un paso atrás!
Estrategia 1
EV = 0, porque tomamos como punto de partida la situación actual. Nos damos por vencido, perdemos la mano, pero no invertimos ni una sola ficha extra.
Estrategia 2: Bluffear en el flop
La expectativa se calcula utilizando la fórmula estándar:

Multiplicamos la probabilidad (p) y el resultado financiero (v) de cada evento y los sumamos:
EV (Bet → Check) = p₁v₁ + p₂v₂
Estrategia 3: Bluffear en el flop y el turn
El cálculo se vuelve más complicado porque tenemos tres resultados posibles. Un fold inmediato de nuestro oponente nos dará el bote inicial. Un call en el flop y un fold en el turn nos dará el bote inicial y una apuesta en el flop pagada por nuestro oponente. Si nos pagan en el flop y en el turn, perderemos ambas apuestas.

EV (Bet → Bet → Check) = p₁v₁ + p₂v₂ + p₃v₃
Estrategia 4: Tres barriles
Aquí hay cuatro escenarios posibles:
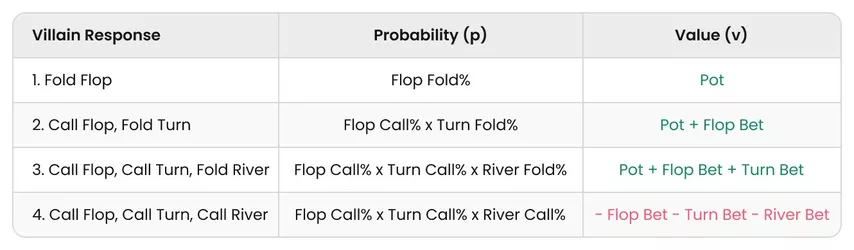
EV (Bet → Bet → Bet) = p₁v₁ + p₂v₂ + p₃v₃ + p₄v₄
Los cálculos son simples, pero monótonos y requieren mucho tiempo; no se pueden hacer sobre la marcha. Para evitar hacerlos manualmente, puede utilizar esta calculadora hecha en Google Docs.
Simplemente agregue el tamaño de su apuesta y el porcentaje de fold en cada calle, y la calculadora le mostrará lo que puede esperar de cada estrategia, basándose en los supuestos mencionados anteriormente.
Ejemplo 2
En el flop tenemos un bluff puro. Nuestro oponente overfoldea en el flop, juega el turn con mucha tenacidad, pero a menudo se asusta en el river.
Ingresamos los tamaños de apuesta y el porcentaje de fold:

El primer paso es convertir el monto de la apuesta en fichas, porque estaremos comparando manzanas con manzanas, es decir, fichas, no porcentajes. Para simplificar, supongamos que el tamaño inicial del bote es uno.

El segundo paso es calcular el valor esperado de cada estrategia:
Estrategia 1:
EV = 0
Estrategia 2: Bluffear en el flop

EV (Bet → Check) = p₁v₁ + p₂v₂ = 0.4 – 0.2 = 0.2
El bluff es rentable y nuestra expectativa es 0.2 del bote original.
Estrategia 3: Bluffear en el flop y el turn

EV (Bet → Bet → Check) = p₁v₁ + p₂v₂ + p₃v₃ = 0.4 + 0.263 – 0.633 = 0.03
La expectativa de los dos barriles es positiva, pero es sólo por 0.03 del bote inicial. Ha bajado notablemente, ya que el oponente defiende con mucha tenacidad en el turn.
Estrategia 4: Tres barriles
No retrocedemos y no nos rendimos:

EV (Bet → Bet → Bet) = p₁v₁ + p₂v₂ + p₃v₃ + p₄v₄ = 0.4 + 0.263 + 0.672 – 0.807 = 0.528
La expectativa de un bluff de tres barriles es de 0.53 del bote original. ¡Esta estrategia resultó ser la más rentable!
Aunque perdimos dinero faroleando en el turn, nuestro segundo barril generó una situación muy rentable: hacer un doble bluff en el river contra un oponente que estaba defendiendo muy tight.

Línea Bet – Check – Bet
Hasta ahora, cualquier check que hiciéramos pondría fin a la mano; simplemente nos estaríamos rindiendo. Pero hacerlo no es en absoluto necesario. Digamos, si su oponente es tan tenaz en el turn, pero overfoldea en el river, ¿por qué no pasar en el turn?
Supongamos que cuando pasamos en el turn, nuestro oponente nos apuesta el 50% de las veces con un rango fuerte con un claro sesgo de valor, contra el cual siempre foldeamos. Si pasa detrás en el turn, su rango se debilita tanto que la probabilidad de que foldee en el river contra nuestra apuesta de un bote completo aumenta al 75%.

EV (Bet → Check → Bet) = p₁v₁ + p₂v₂ + p₃v₃ + p₄v₄ = 0.4 – 0.099 + 0.299 – 0.149 = 0.451
La expectativa de apostar en el flop y el river y pasar (con un posible check-fold) en el turn fue de 0.45 del bote original. ¡No está mal, pero aún así no es tan bueno como con los tres barriles!
Conclusión
En la mayoría de los libros, artículos y vídeos teóricos sobre los conceptos básicos del juego, los autores prestan toda su atención a la versión más sencilla del bluff: en una calle. Las matemáticas en este caso son extremadamente simples; todos los cálculos se pueden realizar directamente durante el juego. Sin embargo, todo cambia si queremos plantearnos un bluff largo de varias calles. Muchos entrenadores se limitan a decir: "El field tiende a overfoldear en el river, así que trata de reducir el juego a líneas con un bluff en el river". Sin embargo, un bluff rentable en el river no siempre compensa bluffs no rentables en el flop y el turn. Es por eso que los cálculos más complejos para bluffs largos son clave para cualquier análisis de las tendencias del field. Cuando esté buscando líneas donde el field hará overfold, no debe mirar cada calle en el vacío. Para encontrar bluffs rentables, tendrá que calcular el EV de toda la línea.
Los cálculos para los bluffs largos no son particularmente complicados, pero sí tediosos. Puede hacerlos manualmente, esto tiene ciertos beneficios, pero de todas formas recomiendo usar una calculadora sencilla que le permita analizar diferentes situaciones de forma rápida y eficiente.
Si no está interesado en analizar bases de datos grandes, aún puede sacar algunas conclusiones útiles:
– los bluffs largos son más riesgosos que los de una sola calle: el riesgo supera significativamente la recompensa, ya que el bote crece en cada calle;
– un bluff rentable en el river no siempre garantiza la rentabilidad de los tres barriles, ya que hay que tener en cuenta las posibles expectativas negativas en las calles anteriores;
– dado que los cálculos de los bluffs largos son difíciles de realizar durante el juego, le aconsejo que los haga en casa cuando trabaje en líneas explotativas;
– no combinar todas las opciones en una fórmula grande y compleja, sino calcular el EV para cada caso por separado, como se muestra en las tablas anteriores;
– la línea más obvia no siempre coincide con la más rentable.
- Mayor rakeback y bonos personales
- Ayuda con depósitos y retiros
- Acceso a aplicaciones móviles
- Resolvemos problemas con cuentas
- Soporte técnico
- Preguntas acerca del sitio y el foro





















