El último as
Imagínese que viene a un casino y le ofrecen jugar un juego nuevo. Quizás no sea lo más interesante, pero aquí están sus reglas: el crupier toma la baraja en sus manos y comienza a voltear las cartas una por una, y debes adivinar cuál será el último, cuarto as de la baraja. Quizás el 25° o el 38°; puede indicar cualquier posición. La baraja está completamente mezclada, la distribución de las cartas es aleatoria. Acertar correctamente el último As paga lo mismo independientemente de la posición que elijas.
Parece difícil idear una estrategia ganadora para un juego como este, ya que los ases pueden terminar en cualquier lugar de un mazo como este. Sin embargo, en realidad tenemos una elección óptima que maximizará nuestras posibilidades de ganar. Esta elección es
la última, la carta 52° del mazo.
Al elegirla, ganarás el cien por ciento de las veces.

Es broma, por supuesto. Simplemente ganarás con más frecuencia que con cualquier otra respuesta. Averigüemos por qué.
En primer lugar, obviamente hay respuestas estúpidas en este juego. No tiene sentido elegir las tres primeras cartas, porque esto, por definición, no le traerá éxito. Incluso si esta carta es un as, definitivamente no será el último del mazo. En teoría, el as que necesitamos podría aparecer en algún lugar entre las cartas 4 y 52.
Digamos que elegiste la carta 38°. En cuatro de 52 casos, se mostrará un as, pero la probabilidad de que sea el último as de la baraja no es del cien por cien. Una diferencia importante al elegir la carta 52° es que al mencionarla, garantizas que el as que salga en esta posición será el último.
Para comprender mejor por qué esto es importante, juguemos con una baraja de seis cartas.

El objetivo de acercar la elección al final del mazo es que cuanto más avancemos, más cartas vimos y la carta que elijamos será el cuarto y último as. Al elegir la cuarta carta, ganamos solo si los tres ases anteriores estaban en las primeras posiciones. Este no es estrictamente un orden único, porque no tenemos en cuenta los palos. Nuestros ases pueden salir en cualquier orden, por lo que tenemos 24 combinaciones ganadoras.
Pero cuando elegimos la quinta carta, necesitamos más órdenes específicos. Los ases se pueden barajar de la misma manera, pero cualquier posición anterior a ellos o entre ellos también puede incluir cualquiera de las dos reinas. Y habrá aún más opciones de victoria a la hora de elegir la sexta carta.
No quiero sumergirme en cálculos para 52 cartas. Aquí, por ejemplo, se muestran todas las combinaciones de una baraja de tres cartas, con dos ases y un rey.

Evidentemente, no tiene sentido elegir la primera carta: nunca ganaremos. Elegir la segunda carta nos traerá la victoria en dos casos de seis. La elección de la tercera carta se produce en cuatro de seis casos. ¡La conclusión es obvia!
Los chistes del joker
Para comprender las condiciones de este problema, basta con saber cómo se determina la fuerza de una mano en el poker. A continuación he ordenado todas las combinaciones por valor, desde la escalera real hasta carta alta.
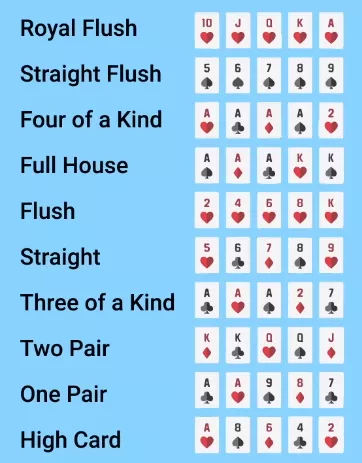
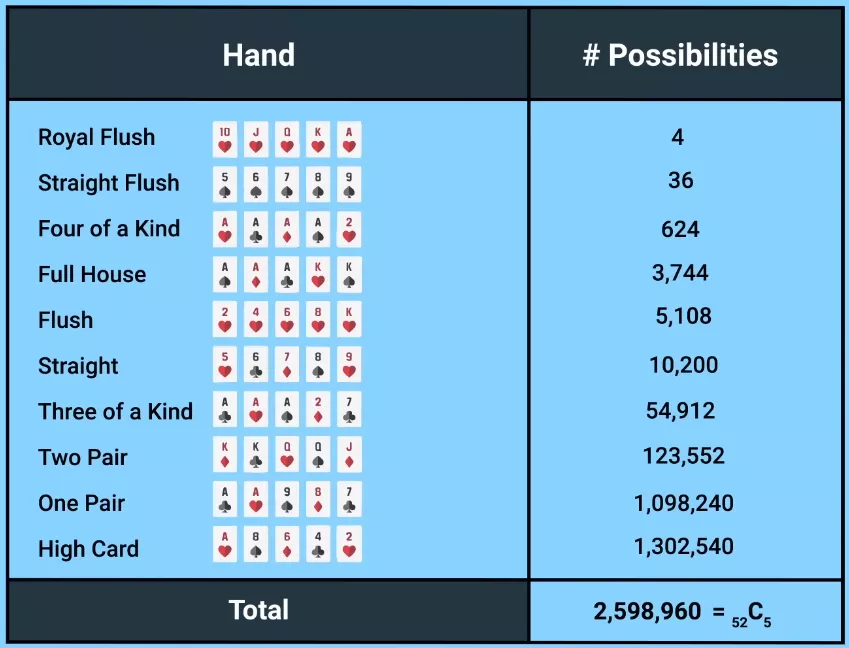
Como la mayoría de ustedes saben, la jerarquía de una combinación está determinada por la probabilidad de que ocurra: cuanto menos frecuentemente ocurre, más fuerte es. Sólo hay cuatro escaleras reales, 36 escaleras de color, 624 combinaciones de cuatro cartas iguales, etc. El número total de combinaciones supera los 2.5 millones.
Imaginemos que añadimos un comodín (joker) al mazo. La baraja ahora tiene 53 cartas en lugar de 52. Una vez que recibas un comodín, puedes convertirlo en absolutamente cualquier carta. Por supuesto, intentarás potenciar tu combinación al máximo. La mano sin comodín obtiene sólo una pareja. Con un comodín: un trío si lo convertimos en un . Transformar al comodín en un también fortalece nuestra mano, pero sólo hasta dos pares; pero nosotros, por supuesto, elegimos una combinación más fuerte.
Y ahora mi pregunta:
¿Debería cambiar la clasificación de las combinaciones cuando jugamos con un comodín y, de ser así, cómo exactamente?
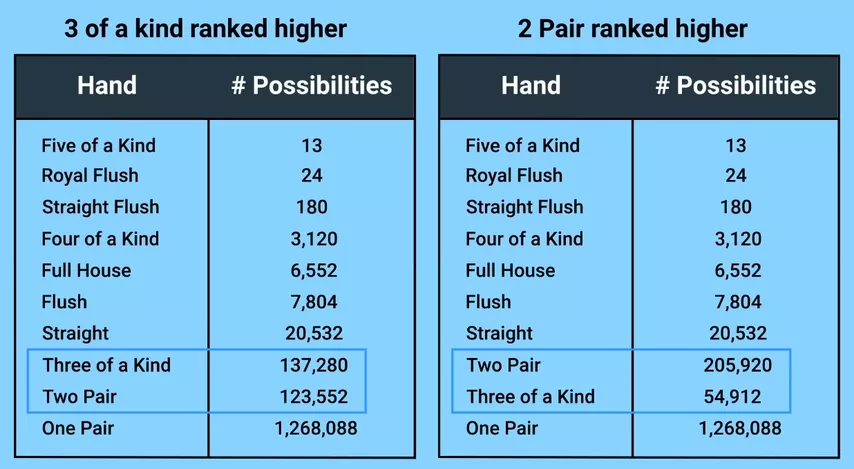
¿Tal vez tener un comodín en la baraja hará que un color sea menos probable que un full? ¿Quizás habrá otros cambios? Una cosa se puede decir de inmediato: la combinación de "cinco cartas idénticas" aparece con el comodín. ¿Qué lugar en la jerarquía ocuparía?
Evidentemente, la primera: el número de combinaciones es igual al número de las cartas de valor de la baraja, 13. Hay seis veces más escaleras reales con comodines, y con 24 combinaciones bajarán al segundo lugar.

Pero no tendremos ningún otro tipo nuevo de manos. Entonces, ¿la clasificación de combinaciones cambiaría debido al comodín, o no?
Espero que hayas tenido tiempo de pensar en esta pregunta, porque ahora te diré la respuesta:
Cuando se juega al poker con un comodín, no hay forma de clasificar las combinaciones según la probabilidad de que ocurran.
¿Por qué sucede esto? Por la paradoja asociada a los tríos y dos parejas.
Supongamos que dejamos sin cambios el orden de fuerza de las combinaciones: los tríos son superiores a los dos pares. En este caso, cada vez que nos reparten un comodín, una pareja de mano y dos cartas más, utilizamos el comodín para fortalecernos y hacer un trío.
Sin el comodín, los trips se podrían formar 54.912 veces. Gracias al comodín, su número aumenta a 137.280.
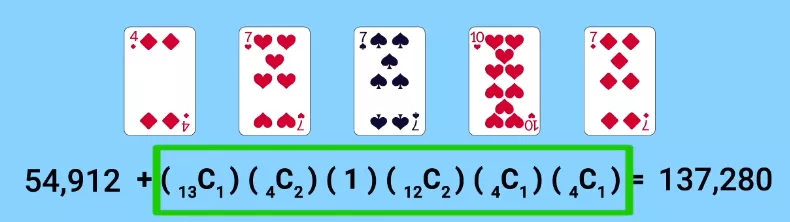
¡Pero esto es más que el número de combinaciones posibles de dos pares! Había 123.552 sin comodín, y este número no cambió después de la introducción de una carta adicional, porque siempre que tenemos la oportunidad de formar dos parejas con ella, preferimos el trío, y las dobles parejas con un comodín siempre se convierten en un full house.
Dado que ahora los dobles pares se encuentran con menos frecuencia que los tríos, es necesario cambiar la jerarquía de las combinaciones. ¡Pero entonces ya no será rentable para los jugadores completar los tríos usando comodines! El número de trips vuelve a los 54.912 originales y el número de combinaciones de dos pares aumenta a 205.920.
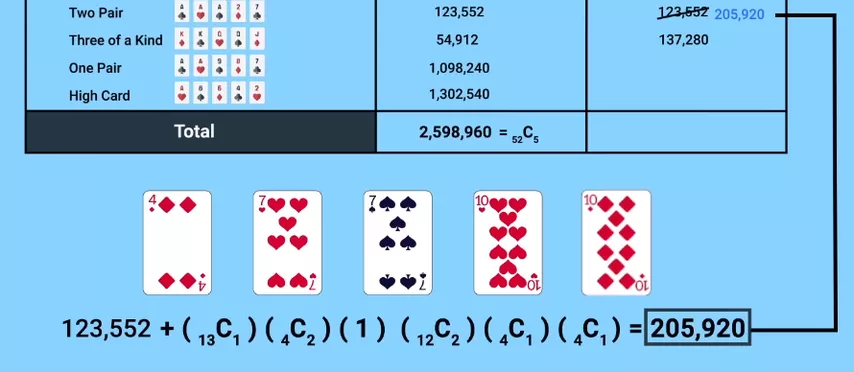
Surge un ciclo interminable y llegamos a una paradoja: resulta imposible finalmente elegir la combinación más alta en función de la probabilidad de que ocurra.
Si estás interesado, aquí tienes las probabilidades de combinaciones al jugar con un comodín:
Juego casi limpio
Te mostraré un juego que a primera vista parece bastante justo, pero que gracias a un algoritmo simple te permitirá ganar al menos dos de cada tres veces y, en condiciones favorables, más de siete veces a uno.
Jugamos con una baraja normal de 52 cartas, la mitad de las cuales son negras y la otra mitad rojas. Participan dos jugadores. El primero selecciona una secuencia de tres cartas y nombra su color, por ejemplo, "roja – roja – negra". Luego el segundo jugador hace lo mismo. Después de eso, comienzan a sacar cartas de la baraja, y gana aquel cuya secuencia salga primero.
Parece que no hay trampa. ¡Bienvenidos al juego Humble-Nishiyama!
En octubre de 1969, Walter Penny publicó un sencillo juego de lanzar una moneda al aire en el Journal of Recreational Mathematics. Pronto Steve Humble y Yutaka Nishiyama trasladaron su juego a una baraja de cartas estándar.
¿Qué peligros podría haber? Bueno, probablemente no deberías elegir una secuencia de tres cartas idénticas, porque la probabilidad de ver una tercera carta roja después de que ya hayan salido dos rojas se reduce ligeramente. ¿Pero qué más? Después de todo, la probabilidad de recibir una carta negra o roja es siempre de aproximadamente 50/50.
De hecho, si excluimos las opciones monótonas de RRR (roja – roja – roja) y BBB (negra – negra – negra), para el primer jugador prácticamente no hay diferencia sobre qué elegir. Sin embargo, el segundo tiene una estrategia de trabajo que garantiza la victoria.
Digamos que el primer jugador eligió BRB. Tomamos la segunda carta de su secuencia, cambiamos el color, la colocamos al principio, retiramos la última carta y el ajuste está listo:
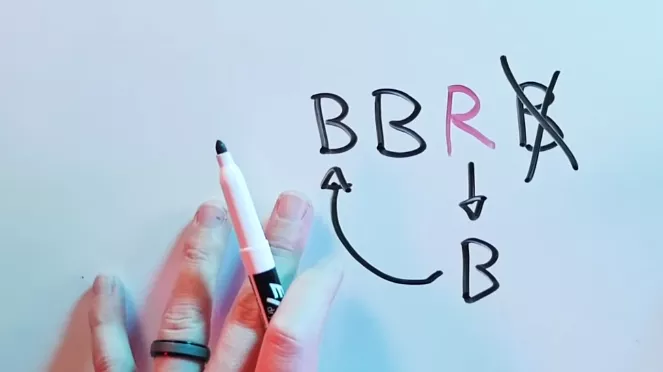
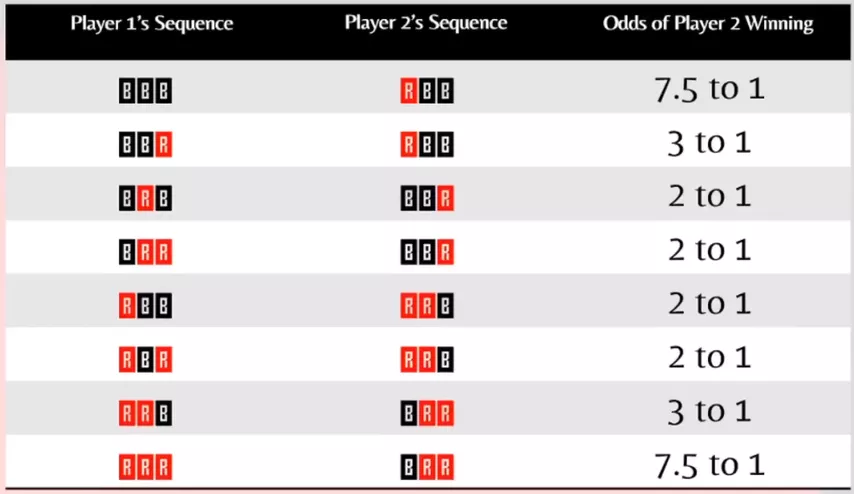
Nuestra ventaja sobre el primer jugador es más convincente de lo que podría sugerir la inocente diversión de la distribución aleatoria de cartas:
Y existe porque este juego pertenece a la clase de los intransitivos.
Ejemplo de transitividad:
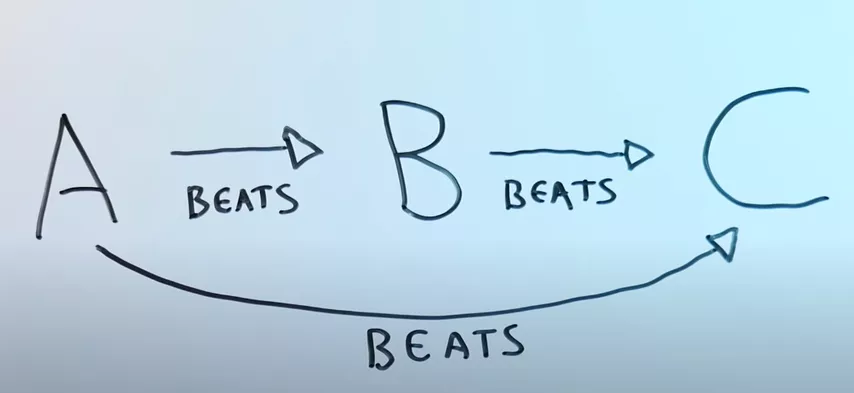
Si le gusta más la pizza que los tacos y prefiere los tacos a la comida enlatada para perros, al elegir entre pizza y comida enlatada para perros, también votará por la pizza. Estas preferencias alimentarias serán transitivas. Sin embargo, si por alguna razón desconocida la comida para perros le sabe mejor que la pizza (¡pero sólo en este escenario!), sus preferencias alimentarias serán intransitivas.
En los juegos no transitivos, el primer jugador no tiene mejor opción. Las relaciones en ellos describen preferencias sobre pares de alternativas, cuya comparación conduce a la presencia de ciclos: A es preferible a B, B es preferible a C y C es preferible a A. El ejemplo clásico es, por supuesto, el piedra, papel o tijeras. Este juego crea un ciclo de posibles elecciones, ninguna de las cuales ofrece la mejor posibilidad de ganar.
El juego Humble-Nishiyama también es intransitivo. Aquí está la jerarquía de los órdenes en este juego:
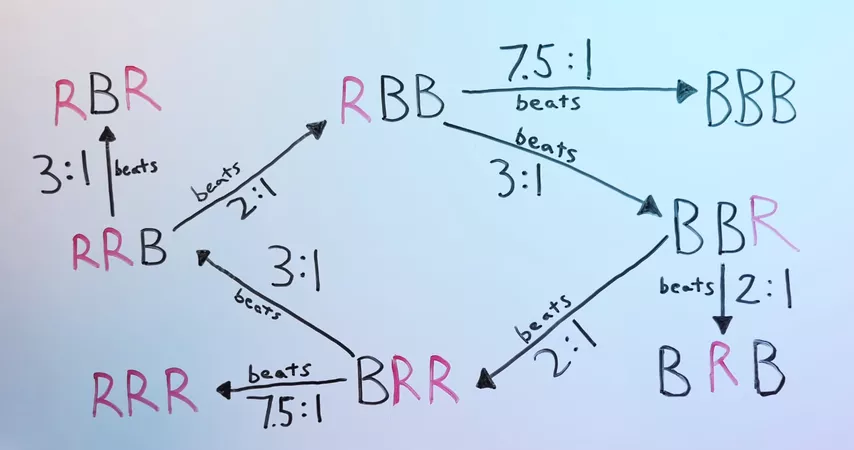
Conociendo la elección del primer jugador, podemos elegir la respuesta más rentable. Y el juego, que a primera vista parecía tan justo, en realidad le da al segundo jugador una gran ventaja.
